활성화 함수
활성화 함수(Activation Function)란?
- 인공 신경망에서 입력 신호의 가중치 합을 출력 신호로 변환하는 함수
- 기본적으로 비선형성(non-Linearity)을 가진다.
우선 활성화 함수의 역할에 대해 알기 전에 선형 함수와 비선형 함수가 무엇인지 알아보자
선형 함수(Linear Function) VS 비선형 함수(Nonlinear Function)
- 선형 함수(Linear Function)란?
- 함수가 직선의 형태를 가지며, 그래프가 직선으로 나타나는 함수
- 입력값이 일정하게 증가하면 출력
- 1차 함수 이며, x에 대한 최고 차수가 1
- 일반적인 형태 ) f(x) = ax + b
- 비선형 함수(Nonlinear Function)란?
- 그래프가 직선이 아닌 곡선으로 나타나는 함수 또는 특정 구간에서 일정한 값을 유지하다가 갑자기 변하는 함수와 같은 계단형 함수(불연속적인 함수)
활성화 함수의 역할(즉, 비선형 함수여야 하는 이유)
- 과적합 현상을 피하기 위해 의도적으로 함수의 그래프 모양을 비틀기 위함
- 퍼셉트론은 기본적으로 선형 모델(연속적인 모델)로 작동해서, XOR 문제 처럼 비선형적인 데이터를 처리하는데는 어려움이 있기 때문
- 퍼셉트론만을 사용한 선형 모델의 경우 연속적인 선의 형태를 띄기 때문에 여러 개의 층을 적용해도 한개의 층을 적용한 것과 같은 결과를 가져올 수 있기 때문에 여러개의 특징들을 뽑아내지 못하기 때문에 활성화 함수를 통해서 비선형 변환을 해준다.






*과적합 현상(Overfitting)이란?
- 훈련 데이터에만 너무 지나치게 맞춰져 일반화 성능이 떨어지는 현상
-> 즉, 학습 시킨 훈련 데이터들에 대해서만 성능이 좋게 만들어져 새로운 데이터(테스트 데이터)에 대해서는 성능이 떨어지는 경우를 말한다.
비선형 함수이기만 하다면 활성화 함수로서 사용가능할까?
- 결론부터 말하자면 아니다
- 예시 ) 비선형 함수로 계단형 함수가 있지만 활성화 함수로 사용하지 않는다
- 신경망은 역전파(Backpropagation)를 사용하여 가중치를 업데이트하는데, 이 역전파를 사용할때 미분(Gradient) 즉, 기울기가 필요하다.
- 그런데 계단형 함수의 경우 기울기가 0이기 때문에 기울기 소실 현상이 발생하기 때문에 사용할 수 없다.




기울기 소실 (Vanishing Gradient) 현상이란?
- 신경망을 학습할때 역전파(Backpropagation) 과정에서 기울기(Gradient, 미분 값)가 점점 작아져서 0에 가까워져서 가중치가 거의 업데이트 되지 않아 학습이 거의 되지 않는 현상
기울기 소실이 어떻게 학습에도 영향을 주게 되는 것일까?
- 역전파란 오차(손실, [학습결과 - 실제 결과]) 를 출력층에서부터 입력층 방향으로 전파하면서, 각 가중치의 변화량(기울기)을 계산하는 과정
-> Chain Rule 기법을 사용해서 수행됨- 즉, 역전파는 손실 함수가 가중치에 대해 얼마나 영향을 받는지를 계산하는 알고리즘
- 역전파를 통해 해당 layer(층)에서의 기울기를 구함
- 이렇게 역전파를 통해 계단된 기울기를 가지고 경사하강법 등을 사용해서 가중치를 업데이트하게 된다.
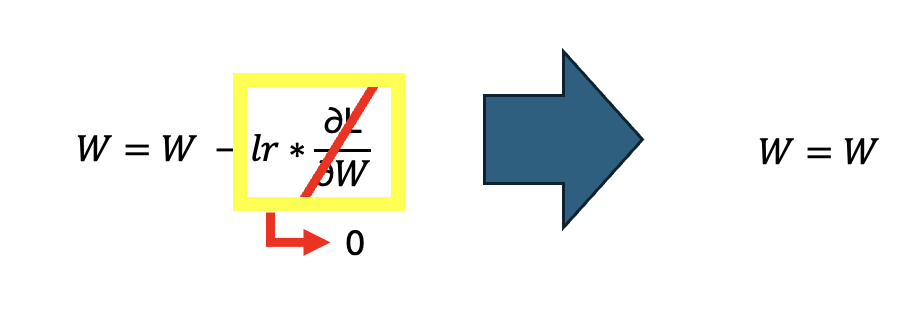
-> optimizer 과정 - 경사 하강법을 사용해 가중치를 업데이트 한다고 가정했을 때 역전파를 진행하다 기울기 소실 현상이 발생하면 ∂L /(∂W) = 0 으로 수렴하게 되어서 이전의 가중치와 변화가 없게 되어서 학습이 안되기 때문이다.


활성화 함수의 종류
- 시그모이드(sigmoid) 함수


-> 실수 값을 받아 0 ~ 1 사이의 값으로 압축하는 함수
-> 단점 1) 기울기 소실 문제(Vanishing Gradient Problem)가 발생
=> 시그모이드 함수의 기울기는 입력이 0일때 가장 크고 |x| 가 클수록 기울기는 0에 수렴하기 때문
-> 단점 2) 시그모이드 함숫값은 0이 중심(zero-centered)가 아니다
=> 학습 속도가 느려진다.
why? 출력이 0과 1 사이로 제한되다 보니 출력값이 0.5에서 멀어질수록 기울기(∂L /∂W)가 급격히 작아져서 학습속도가 너무 늦어진다.
- Tanh 함수


-> 실수 값을 입력받아 -1 ~ 1 사이의 값으로 압축하는 함수
-> 0을 중심으로 대칭 관계(Zero-centered)에 있는 함수이기 때문에 Zig-Zag 현상(곧바로 최적화 값에 도달하지 못하고, 돌아서 최적화 값에 도달하는 현상)이 덜하여서 시그모이드에 비해 최적화를 잘한다.
=> 시그모이드와 같이 기울기 소실 문제를 가지고 있다.
- ReLU 함수


-> 입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하이면 입력을 출력하는 함수
-> 양의 구간에서 Not satuated(양의 구간에서 기울기가 0으로 수렴하지 않는다.)
-> exp(e)가 없어서 연산이 빠르다
=> 가장 많이 사용되는 활성화 함수
- Leaky ReLU 함수


-> a 값의 범위는 보통 0.01 ~ 0.3 사이의 값으로 설정된다.
-> 일반적으로 a=0.01을 주로 사용
- Exponential LU 함수
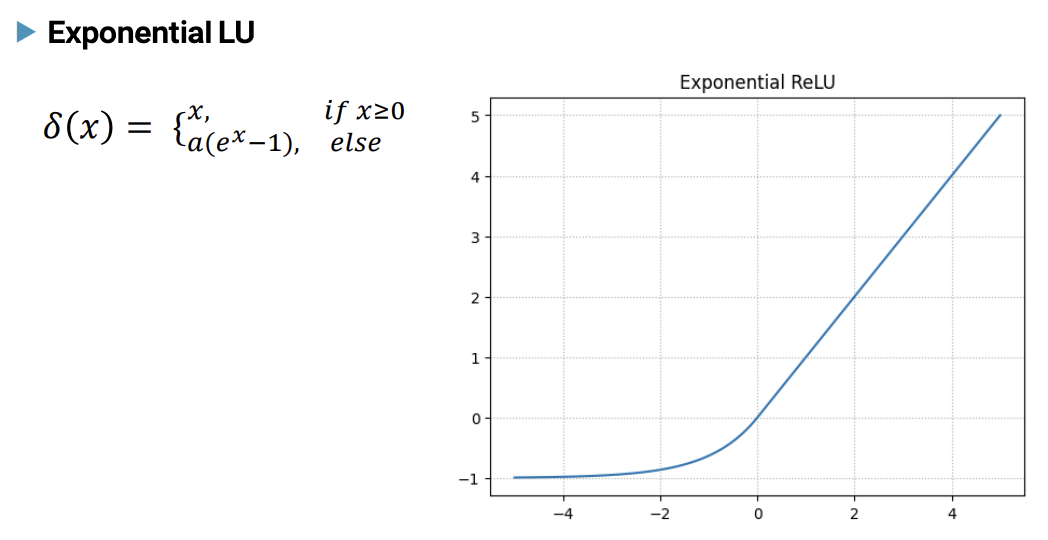

-> a 의 값은 양의 실수로 주로 0.1 ~ 1 사이로 설정된다.
-> 일반적으로 a =1 을 많이 사용
- Softmax / LogSoftmax 함수
- 주로 다중 분류에서의 출력층에서 사용되는 함수
-> Logsoftmax를 거진 후에 one-hot encoding 작업을 수행 - 결과 값들에 대해서 확률 값을 구하고자 할때 사용하는 함수
- 0~ 1 사이의 값들로 모두 정규화되며 총합은 항상 1이 되는 특성을 가진 함수
- 주로 다중 분류에서의 출력층에서 사용되는 함수



-> LogSoftmax는 Softmax에 Log가 붙은 형태의 함수이다.
활성화 함수를 딥러닝 과정 중에 언제 적용해서 사용할까?
- 순전파(Forward Propagation) 과정에서 적용된다.
- 신경망을 통해 여러 층을 거칠 때마다 각 층에서 계산된 출력 값에 활성화 함수가 적용되어 다음 층으로 전달된다.
-> 퍼셉트론 계산 후에 적용
