Overfitting+ Internal Covariate Shift와 해결 방법
과적합(Overfitting)
모델이 학습 데이터에 과도하게 적응하여 일반화 성능이 저하되는 현상
-> training-set에 너무 과하게 모델이 최적화된 상태
-> 모델이 overfitting되면 training-set에서는 정확도가 매우 높게 나오지만 test-set에서는 낮은 정확도가 나온다. 한마디로 범용성이 없는 모델이 된다.
- 원인
- 복잡한 모델 구조
- 모델의 파라미터 수가 너무 많아 학습 데이터에 과도하게 적응함
- 데이터 부족
- 데이터가 부족하여 노이즈까지 학습함
- 잘못된 학습 설정
- 학습 Epoch가 너무 많아 과학습 발생
- 복잡한 모델 구조

<과적합 해결방법>
1. 데이터를 추가 수집
- 데이터의 양이 많고, 다양할 수록 모델의 범용성은 더 높아진다.
2. Feature(입력 데이터의 중요한 속성) 축소
데이터를 설명하는 feature 중에는 관계성이 적거나 없는 즉, 쓸모없는 feature를 제거해주는 작업
- 예시로 주어진 데이터로부터 장미인지 해바라기인지를 판단하는 모델을 만든다 했을때 feature 항목으로
- 가시의 여부
- 꽃의 색깔
- 개화 시기
- 잎의 개수
- 이렇게 있다 했을떄 1,2,3 은 장미를 구분하는데 유효한 특징(feature)라는 것은 명확하지만 잎의 개수는 변별성이 없는 특징이다 이런 feature 들을 제거해줌으로써 overfitting현상을 감소시킬 수 있다.
2. 데이터 증강(Data Augmentation)
학습 시마다 개별 원본 이미지를 다양한 방법으로 변형해서 학습하는 것 -> 데이터 부족 문제를 해소 할 수있다.
-> 이때 새로운 데이터는 원본 데이터의 특성을 잘 반영하고 있어야한다.
-> 주로 이미지 학습할 때 사용
- 데이터 증강의 필요성
- 훈련 데이터를 얻는데 많은 비용이 필요하다. -> 데이터 부족 문제 해결
- ex. 자동차 사고, 의료, 군사 등
- 작은 데이터 세트에 대해 과적합을 일으키기 때문에 필요하다. -> 과적합 방지
- 불균형 데이터 문제 해결을 위해 필요 -> 모델의 일반화 향상
-> 불균형 데이터란 훈련 데이터와 테스트 데이터의 분포가 다른것 즉 성질이 다르다.
- 훈련 데이터를 얻는데 많은 비용이 필요하다. -> 데이터 부족 문제 해결
- 이미지 데이터 증강 종류
- 기하학적(Geometry) 변환
- 회전(Rotation), 이동(Translation), 크기 조정(Scaling)
- 뒤집기(Flip) : 이미지를 수평이나 수직으로 뒤집어 새로운 시점에서의 이미지를 생성
- 컬러 조절
- 밝기 조절(Brightness Adjustment) : 이미지의 밝기를 조절하여 다양한 조명 상태를 조절
- 노이즈 삽입
- 블러링(Blurring)

3. 정규화(Regularization) ->Weight decay
학습 과정에서 가중치에 패널티(규제)를 부여함으로써 학습 데이터의 정확도(training accuracy)를 낮추고, 평가 데이터의 정확도(testing accuracy)를 높이는 것
-> 가중치 W가 클수록 더 큰 패널티를 부과해 학습 데이터들에 대해서 지나치게 fit하지 않도록 조절하는 것
=> 지나치게 fit하지 않도록 == Loss 값을 늘려준다.
-> 패널티를 얼마나 부과 할 것인지는 L1/ L2 regularization 공식에 따라 계산함
- 모델의 일반화 성능을 높여 overfitting을 예방하는 방식
- L1/L2 정규화(Weight Decay)를 적용하여 가중치 크기 제한
- L1 규제 : 가중치의 절대 값을 최소화하는 것을 목표로 한다.

- L2 규제 : 가중치의 제곱을 최소화하는 것을 목표로 한다.


4. 드롭아웃(Drop out)
훈련(training) 중에 무작위(랜덤)로 "탈락"하거나 특정 비율의 뉴런을 제외하는 방법
단, overfitting을 방지하기 위한 방법이므로 train-set에만 적용되고, test-set을 예측할 때는 사용되지 않는다.
-> 학습 시에만 사용
- 컴퓨터 비전에서는 충분한 데이터가 부족하기 때문에 대부분 Drop out 사용
- 학습 시에 인공 신경망이 특정 뉴런 또는 특정 조합(+기능)에 너무 의존적이게 되는 것을 방지해주고, 매번 랜덤 선택으로 뉴런들을 사용하지 않으므로 서로 다른 신경망들을 앙상블하여 사용하는 것 같은 효과를 내어 과적합을 방지해준다.
- 앙상블(Ensemble) 방법 : 여러 단순한 모델을 결합하여 정확한 모델을 만드는 방법
- 고려해야할 사항
- dropout_ratio(삭제 비율) : 각 훈련 반복 중에 탈락 되는 뉴런의 비율은 일반적으로 약 0.2 ~ 0.5에서 시작
- 삭제 비율이 너무 낮으면 과적합을 효과적으로 방지할 수 없음
- 삭제 비율이 너무 높으면 학습을 방해 할 수 있다.
- Drop out 위치
- 원칙적으로 히든 레이어에 드롭아웃을 적용하는 것으로 제한
- 다른 정규화 기술과의 상호 작용
- 가중치 감소(Weight decay)와 같은 다른 정규화 기술과 함께 사용되는 경우가 많다.
- dropout_ratio(삭제 비율) : 각 훈련 반복 중에 탈락 되는 뉴런의 비율은 일반적으로 약 0.2 ~ 0.5에서 시작
- 사용 이유
- 앙상블 효과
- 테스트시 모델이 모든 뉴런을 사용하므로 드롭아웃 방식을 통해 앙상블 효과를 일으켜 여러 하위 네트워크의 예측을 효과적으로 일반화 해서 모델의 예측력을 향상시킨다.
- 동시 적응 감소
- 알 수 없는 유닛의 공동 적응을 방해하며 뉴련은 특정 유닛의 존재에 의존할 수 없으므로 더 다재다능하고 적응력이 높아진다.
- 노이즈 주입
- 드롭아웃의 확률론적 특성은 학습과정에 노이즈를 주입하는 것과 같이 볼 수 있고, 이 노이즈는 정규화 역할을 하여 모델이 훈련 데이터에 너무 가깝게 피팅되는 것을 방지하고 노이즈가 마치 신호인것처럼 처리한다.
- 앙상블 효과

5. 적절한 모델 크기 사용 : 데이터 크기에 맞는 모델 선택
6. 조기 종료(Early Stopping) : 검증 데이터 손실이 증가하면 학습 중단
Covariate Shift 현상 -> 입력층에서의 문제
-> 데이터 불균형
훈련 데이터(train)와 테스트 데이터(test)의 입력 데이터 분포가 다를때 발생하는 문제
모델이 학습한 입력 데이터와 실제 예측해야하는 입력 데이터의 특성이 달라지면서 성능이 저하되는 현상 -> 과적합으로 이어질 수 있다.
왜 발생할까?
- 데이터 수집 방식이 달라짐
- 훈련 데이터는 고급 카메라로 찍은 사진이고, 테스트 데이터는 일반 스마트폰 사진일 경우 사진에서의 성능 차이로 인해 발생할 수 있음
- 시간이 지나면서 데이터 분포가 바뀜
- 경제 트렌드가 변하면서 과거의 데이터 패턴이 더이상 유효하지 않을 경우
- 데이터의 특정 조건이 변함
- 의료 AI 모델을 학습할 때, 미국 병원의 환자 데이터를 사용했는데 실제 사용 환경에서는 아시아 병원의 환자 데이터를 예측해야하는 경우 환자의 특징이 다를 수 있기 때문에 모델 성능이 저하 될 수 있음
- 특정 클래스 데이터가 불균형하게 포함됨

-> 훈련 데이터와 테스트 데이터의
Internal Covariate Shift -> 딥러닝에서 발생하는 현상
Layer마다 동일한 조건으로 학습할 때, Internal Covariate Shift 현상으로 데이터 분포가 Layer마다 다르게 되어 뒷단에 위치한 Layer일 수록 변형이 누적되어 input data의 분포가 많이 달라지는 현상
->딥러닝 학습 과정에서 각 층의 입력 분포가 지속적으로 변화하는 현상
- 이는 학습 속도를 저하시키고 불안정한 학습을 유발 -> 불안정한 학습은 곧 과적합을 유발할 가능성이 있다.
- 신경망에서 층이 많아질 수록(깊어질 수록), 앞쪽 층에서 가중치가 변화할 때 뒤쪽 층의 입력 분포가 급격히 변함

<Internal Covariate Shift 해결 방법>
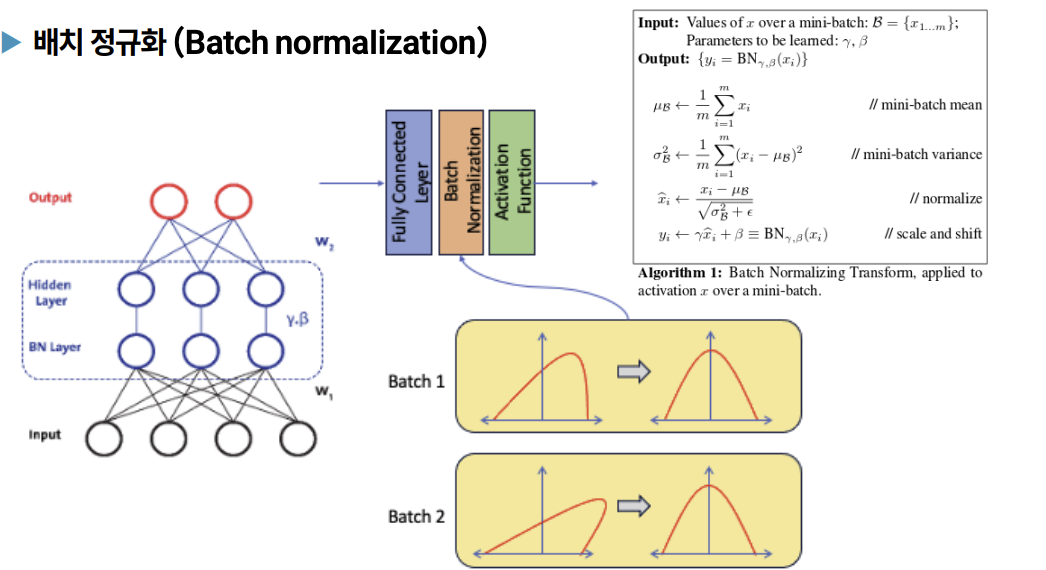
배치 정규화(Batch Normalization) -> 주로 Convolution layer에 적용 많이 함
- 미니 배치 단위로 데이터의 분포를 정규화하여 학습 안정성과 속도를 향상
- 각 층의 입력을 미니 배치 단위로 정규화하여 분포 변화를 줄임
- 즉, 각 레이어마다 정규화하는 레이어를 두어 변형된 분포가 나오지 않도록 조절하는 것
- 장점
- Internal Covariate Shift 완화
- 학습 속도 증가
- 과적합 방지