손실 함수 그래프 표현



손실함수를 3D 또는 그 이상의 차원 그래프로 나타낸 첫번째 그림을 등고선으로 나타낸 것이 두번째 그림(등고선 그래프)이다.
등고선이란? 같은 높이의 것들을 선으로 연결한 것
하지만 첫번째 그림과 같은 경우는 우리가 원하는 이상적인 모델이고 일반적인 딥러닝을 학습할때는 손실함수 그래프는 여러개의 변수와 그 변수에 대한 다항 함수 등과 같이 3번째 그림과 같은 복잡한 차원 그래프로 나타난다.
-> 이러한 손실 함수에서 모든 구역에서의 Minimum 즉, Global Minimum에 도달 할 수 있는 파라미터(W,b)를 구하는 것이 딥러닝의 목적이고, 그것에 도달할 수 있도록 하는 방법이 Optimizer 함수들이다.
Optimizer 함수란?
함수의 값이 낮아지는 방향으로 각 독립변수들의 값을 변형시키면서 함수가 최솟값을 갖도록 하는 독립변수의 값을 탐색하는 방법
-> 손실함수의 모든 구간에서의 최솟값으로 가기위한 W,b를 구하기 위한 함수
- Optimizer 함수의 종류
- GD, SGD, Mini-batch Gradient Descent, momentum, RMSprop, Adam 등
학습률 (Learning rate) -> 주로 α를 사용
- 학습률은 주로 0~1 사이의 값을 사용
- 학습률을 사용하는 이유
- Gradient의 크기가 너무 커서 섣불리 Gradient 방향으로 휙 가버리는 현상을 막기 위해서 곱해준다.
- 진동이나 벗어날 수 도 있어서 위험하기 때문
- 왜 학습률과 Gradient에 (-) 를 붙여줄까?
- Gradient의 반대 방향으로 가야 최소점에 도달할 수 있기 때문

경사하강법이란?
손실 함수의 기울기를 구하고 해당 경사의 반대 방향으로 계속 이동시켜 극값에 이를때까지 반복시키는 것을 말함
- 경사하강법 단계
- 초기값 설정 : 파라미터를 임의로 초기화 -> 0에 가깝게 초기화
- 기울기 계산: 현재 위치에서 함수의 기울기(미분 값)을 계산
- 파라미터 업데이트 : 계산된 기울기의 반대 방향으로 파라미터를 업데이트
- 반복 : 기울기를 계산하고, 파라미터를 업데이트하는 과정을 반복
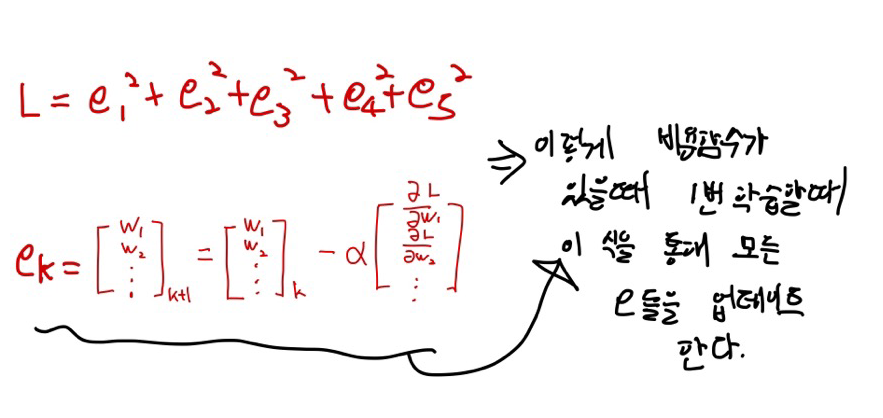
- 경사하강법 식

- 경사 하강법의 종류 -> 위의 식을 통해 출력층의 노드(e) 몇 개의 파라미터(w,b)를 변경해 L에 반영해주느냐에 따라 3가지로 구별됨
- 경사하강법 (Gradient Descent)
- 확률적 경사 하강법( Stochastic Gradient Descent, SGD)
- 미니 배치 경사 하강법(Mini-batch Gradient Descent)
- 모든 경사하강법의 단점 : 지역 최솟값에 빠질 수 있고, 학습률에 따라 수렴에 영향을 줌
경사 하강법(Gradient Descent) : 전체 훈련 데이터를 한번에 사용하여 기울기를 계산
- 장점 : 전체 데이터에 대한 정확한 기울기를 계산하므로 안정적
- 단점 : 데이터가 많을 경우 계산 비용이 크고, 메모리 사용량이 많음
-> 한번 학습할때 모든 파라미터의 기울기를 한번에 다 고려해서 움직이기 때문에 굉장히 느리다
-> 손실함수에서 가장 가까운 Minimum 값으로 수렴하게 됨
=> 문제 : Local Minimum 값으로 수렴하게 되어 학습이 제대로 안된다.

-> 이러한 GD의 문제점을 해소하고자 나온것이 SGD이다.
확률적 경사 하강법(Stochastic Gradient Descent, SGD) : 훈련 데이터에서 하나의 샘플을 랜덤하게 선택하여 기울기를 계산
-> 랜덤하게 데이터 하나씩 뽑아서 loss만듬 (랜덤이라 stochastic)
즉, 하나만 보고 빠르게 방향 결정
-> 모든 데이터를 포함해서 기울기를 업데이트하는 것이 아니라 하나의 데이터만을 반영해서 기울기를 업데이트하는 것
-> 주머니에서 하나를 뽑아서 기울기 계산 후 내려놓는다(비복원 추출) 주머니에 있는 e들을 다 뽑아서 기울기를 갱신했다면 뽑았던 e들을 다시 주머니에 넣고 처음부터 다시 시작
-> local minimum으로부터 탈출의 기회가 되기도 한다. -> 무조건 탈출은 X
- 장점 : 계산 속도가 빠르고, 메모리 요구 사항이 적음
- Local minmum에 빠질 수도있지만 빠져나갈 가능 성 또한 생긴다. 하나의 데이터(e)에 대해서 기울기가 업데이트되기 떄문
- 단점 : 각 업데이트에서 정확한 기울기를 구할 수 없으므로 학습과정이 불안정



-> 한 번 학습할 때 한개의 e의 기울기들만을 반영하기 때문에 너무 성급하게 결정하기 때문에 학습과정이 불안정해진다.
- 왜 gradient가 +를 향하지 않을까?
- 위 그림의 등고선은 모든 데이터를 반영한 등고선이기 때문에 하나의 데이터(e) 를 뽑아서 해당 손실 함수에서의 최솟값을 향해서 기울기가 반영한다면 아래의 그림처럼 이동하게 되어서 결국에는 위의 그림과 같은 방향성을 띄게 된다.

=> SGD는 하나씩만 보니까 너무 성급하게 방향을 결정해서 학습이 불안정해진다. 그래서 나온 것이 아래 내용이다.
미니 배치 경사 하강법(Mini-batch Gradient Descent) : 훈련 데이터를 작은 배치로 나누어 각 배치에서 기울기를 계산
-> 미니 배치 사이즈를 정해주고, 그 개수만큼 랜덤으로 뽑고, 내려놓고, (비복원추출) 다시 배치 사이즈 만큼 다시 뽑고, 다 뽑았으면 다시 다 넣고 해당과정을 반복한다.
-> 미니 배치 경사 하강법은 SGD와 GD 사이의 알고리즘이다.(-> SGD와 GD의 절충안)
-> batch 사이즈를 키울수록 error가 낮아진다. 왜냐하면 GD에 가까워지기 때문
-> batch 사이즈를 낮출수록 error가 높아진다. 왜냐하면 SGD에 가까워지기 때문
- 장점 : 배치 경사 하강법의 안정성, 확률적 경사 하강법의 속도를 가짐
- 단점 : 배치 크기 선택에 따라 성능이 달라질 수 있음


위의 그림에서 파란색이 GD, 보라색이 SGD, 초록색이 MSGD(또는 MBGD라 부름)를 의미한다.
MSGD의 문제점
- 진동 문제 : MBGD는 여러 데이터 샘플의 평균적인 그래디언트를 사용하지만, 여전히 일정 수준의 노이즈가 존재
- 이 때문에 경사가 급격하게 변하는 방향에서 진동하면서 비효율적인 이동이 발생
- 특히, 곡면이 가파른 경우 지그재그로 이동하면서 학습 속도가 느려짐
- 느린 수렴(Slow Convergence) : 일반적으로 학습 후반부(최적점 근처)에서는 그래디언트의 크기가 작아져서 업데이트가 느려짐
- 일정한 학습률을 유지하면 빠르게 수렴할 수 없고, 학습률을 너무 낮추면 학습이 오래 걸림
=> MSGD를 사용하더라도 지역 최소점에 수렴하거나 매우 느리게 빠져나올 가능성이 높음
이러한 MBGD의 진동 문제, 더 빠르게 최적점에 도달하기 위해서 나온것이 이전 gradient의 값을 반영하여 관성 효과를 주는 Momentum이 나오게 되었다.
Momentum(관성, 운동량) -> 시점(시간 축)을 생각해야함

-> 그라디언트를 누적함으로써 관성을 가지게 됨 => 마치 치타 처럼
-> 좌우 방향으로 상쇄되고, 앞으로는 쭉커진다(계속 + 된다).
-> 누적이 같은 e에 대해서 과거 시점의 그라디언트를 누적한다.
-> 보통 SGD나 Adam 등에 Momentum을 적용해서 같이 사용한다.
- 진동을 줄이고, 더 부드럽게 수렴 -> 진동 감소
- 최적점 근처에서도 수렴 속도를 높일 수 있음 -> 빠른 수렴
- local minimum에서 빠져나오기 쉬워짐


하지만 Momentum에도 여러 개의 문제들이 있었다.
- 학습률(learning rate) 설정의 어려움
- Momentum을 사용하면 gradient(그래디언트)의 업데이트가 부드럽게 이어지지만, 여전히 모든 방향에서 동일한 학습률을 적용한다.
- 곡면이 비대칭(ex. 좁고 긴 골짜기)한 경우에는 학습률을 방향별로 다르게 설정하는 것이 더 효율적임
- 학습 속도의 비효율성
- Momentum은 방향성을 유지하여 빠르게 이동하지만, 곡률(curvature)이 큰 지역에서는 여전히 큰 진동을 보일 수 있음
- 특히 가파른 방향에서는 업데이트가 너무 커지고, 평평한 방향에서는 너무 느려지는 문제 발생
- 고차원의 경우 안장점(Saddle Point)에서의 학습 속도 느려지거나 멈출 가능성이 있음
- 평탄한 영역에서 여전히 수렴 속도가 느려짐
- 안장점이란? 다변수 함수의 그래프에서 나타나며 아래의 그림에서 보듯이 어떤 점에서 어느 한 축에서는 극대에 이르면서 다른 축에서는 극소에 이르는 점(검은 점)( => 대표적인 그래프 인 쌍곡 포물면이 말에 장착하는 안장을 닮아서 붙은 이름)

-> 기울기가 0이지만 극 값이 아닌 지점
-> A-B 사이에서 안정점은 최솟값이지만 , C-D 사이에서는 최댓값이다.
-> 따라서 미분이 0이지만 극 값을 가질 수 없다.
=> 경사하강법들은 미분이 0일 경우 더이상 파라미터를 업데이트하지 않아, 안장점을 벗어나지 못하는 한계가 있다.
이러한 Momentum의 문제를 해결하기 위해 NAG와 상황에 따라 학습률을 조절하는 알고리즘인 Adagrad, RMSprop이 나오게 되었다.
NAG (Nesterov Accelerated Gradient)
-> 기본 적인 경사 하강법에 모멘텀을 추가하여 보다 빠르고 효율적으로 최적 점을 찾는 방법
-> 기존의 모멘텀 방식을 개선하여 기울기를 계산하기 전에 먼저 모멘텀에 의해 예측된 우치로 이동한 후 그 지점에서의 기울기를 사용
-> "시점" 차이
- 모멘텀보다 더 개선된 방법으로, 한 단계 앞을 미리 고려하여 이동(현재 위치가 아닌, 미리 예측한 위치에서 기울기 계산)
- 일반 모멘텀 방식보다 더 정확하게 최적점에 도달할 수 있도록 도와준다.
- 불필요한 방향으로 가는 것을 줄이고 더 빠르게 수렴
- 장점
- 학습 과정에서 발생할 수 있는 진동을 감소시키고, 보다 빠른 수렴을 가능하게 한다.
- 딥러닝 모델의 학습 속도를 향상시키는데 효과적

Adagrad (Adaptive Gradient)
-> 매개변수 별로 학습률을 자동 조정하는 최적화 알고리즘
-> 각각의 파라미터마다 빈도 수에 따라 학습률을 조절해주는 것
-> 여기서 "빈도 수"란 gradient의 값이 크면 빈도 수가 크다는 것을 뜻한다고 볼 수 있다.
-> 단순 평균처럼 기울기 제곱을 누적합 이전 기울기들을 다 누적해서 모두 동일하게 반영하여 학습률을 조절
=> 계속 누적이 되기떄문에 파라미터 학습률이 너무 작아질 수 있음
- 학습률을 변수 별로 다르게 조정해주는 방식
- 자주 업데이트 되는 변수는 학습률 감소, 드물게 업데이트 되는 변수는 학습률 유지
- 문제점: 학습률이 너무 작아져서 후반부 학습이 어려워질 수 있음
-> 과거 그래디언트 제곰을 무한히 누적하므로 학습률이 계속 줄어들 수 있다. 이로 인해 학습이 일찍 멈추거나 최적의 성능에 도달하지 못할 수 있다.

-> Gt : 지금까지의 기울기 제곱합
-> 시간이 갈수록 Gt는 점점 커지기 때문에 분모가 계속해서 커져 학습률이 점점 줄어들어 학습이 빨리 멈춰버리는 문제를 초래할수 있다.

RMSprop
-> Momentum을 포함하지 X
-> Adagrad의 문제점을 개선하여 학습률이 너무 작아지는 것을 방지
-> 기울기의 변화량을 지수 이동 평균으로 조절하여 안정적인 학습가능
-> 지수 이동 평균이란? 최근 값일 수록 더 큰 비중을 주고, 옛날 값일 수록 점점 비중을 작게 주는 평균 방식
->최근 기울기에 더 집중해서 학습률을 조절하는 방식


Learning rate를 각 파라미터 별로 다르게 조절하여 가파른 방향에서는 학습률을 줄이고, 평탄한 방향에서는 학습률을 키우는 방식(평준화를 통해 공평하게 탐색)
즉, 학습률을 조절해 경사가 완만한 곳은 과감히 가고 경사가 가파른 곳은 조심히 가자
-> 경사가 완만하다는 것은 그 길로 가도 loss가 잘 변하지 않는다.
-> Global minimum으로 갈 확률이 높아진다.
-> 최근 Gradient의 크기를 반영해서 Gradient를 변경
-> 최근 그래디언트(Gradient) 크기의 평균을 유지하며 학습률을 자동 조정함
- 특징
- 방향별 학습률 조정 -> 곡률이 큰 경우에도 안정적으로 학습 가능
- 진동 감소 -> 학습이 불안정한 지역에서도 균형 잡힌 학습
- 안장점(Saddle Point)에서 빠르게 탈출 가능
RMSprop은 학습률 조절은 되지만 방향성이 부족하다는 문제점이 있다 이러한 문제를 해결하기 위해 나온 것이 Adam이다
Adam(Adaptive Moment Estimation)
-> 모멘텀 + RMSProp
RMSprop과 Momentum을 결합한 것으로, 각 방향별 학습률을 조절하면서도 관성을 유지하여 빠르고 안정적인 학습을 가능하게 하는 방법
->1차 모멘트(기울기 평균)와 2차 모멘트(기울기 제곱 평균)를 활용하여 최적화
- 특징
- Momentum처럼 관성을 유지하여 안정적인 방향으로 이동
- RMSprop처럼 각 방향별 학습률을 조절하여 빠르게 최적화
- 딥러닝에서 가장 많이 사용되는 최적화 알고리즘

-> 그림에서 보는 것처럼 데이터셋의 개수가 많이 늘어나도 학습시키는데 드는 비용이 Adam이 젤 적게 들어서 효율적이라는 것을 볼 수 있다.
최적화(Optimizer) 함수들 비교

- 안장점에서의 각 최적화 알고리즘 상황

-> SGD는 안장점에서 탈출 못한다.
-> Momentum은 첨에는 안장점 근처에서 앞으로 가는 관성이 있어서 앞으로 가다가 뒤로 가는 관성때문에 뒤로 가다가 아래쪽으로 빠지는 Gradient가 생겨서 밑으로 빠르게 쭉 빠지게 된다.
-> RMSprop은 시작하자마자 너무 가파라서 왼쪽으로 휘게 되고 아래로 너무 가파라서 조금씩 이동하게 된다.

-> SGD는 굉장히 느리게 도달하려 한다.
-> Momentum은 관성으로 와리가리 가다 별에 도달하게 됨
-> RMSprop은 첨에 완만한 지역에서 빠르게 가다가 별에 도달할때 쯤 가파라서 천천히 이동하다 도달하게 된다.
- 별(Global Minimum)에 도달하기 직전 RMSprop이 떨리는데 그 이유는?
-> RMSprop 식에서 분모의 입실론이 작아서 분모가 분자보다 더 빠르게 0에 수렴하게 되어서 그 결과 학습률이 갑자기 커져서 가중치 업데이트가 불안정해지고 갑자기 튀는 현상이 발생할 수도 있다.

'AI 정리' 카테고리의 다른 글
| Overfitting+ Internal Covariate Shift와 해결 방법 (0) | 2025.03.19 |
|---|---|
| 파라미터(w,b) 초기 값 정하는 방법 (1) | 2025.03.19 |
| 역전파 (0) | 2025.03.17 |
| 비용 함수 (0) | 2025.03.10 |
| 활성화 함수 (0) | 2025.03.09 |